数据结构:二叉树
一,基本概念
二叉树(BinaryTree)是每个节点最多有两个子树的树结构。通常子树分为左子树和右子树,如图:

二,特性
在二叉树的第i层上最多有2^(i-1)个节点(i>0)
深度为k的二叉树最多有2^k-1个节点(k>0)
对于任意一颗二叉树,如果度数为0的节点数为a,而度数为2的节点总数为b,则a=b+1*(度:一个节点含有的子树的个数称为该节点的度)*
具有n个节点的完全二叉树的深度必为:log2(n+1)(以2为底的(n+1)的对数)
对于完全二叉树,如果按照从上至下从左至右的数组顺序从0开始编号,对于编号为i的节点:
1
2
3
4
5
6
7
| (1). 若i>0,i 位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
(2). 若 2i+1< n,左孩子序号: 2i+1;否则无左孩子
(3). 若 2i+2< n,右孩子序号: 2i+2;否则无右孩子
|
三,两种特殊的二叉树
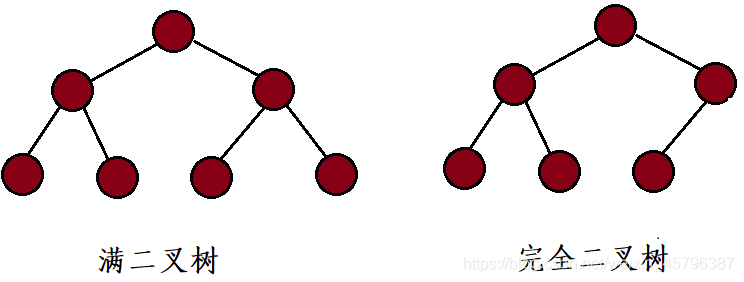
1,满二叉树:
除叶节点外每一个节点都有左右子节点,且叶子结点都处在最底层
2,完全二叉树:
对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 满二叉树是一种特殊的完全二叉树。
四,二叉树的创建与遍历
创建:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| # 节点类
class Node(object):
def __init__(self, elem, lchild=None, rchild=None):
self.elem = elem # 本身值
self.lchild = lchild # 左孩子
self.rchild = rchild # 右孩子
# 树类
class BinaryTree(object):
def __init__(self, root=None):
self.root = root # root为根节点
def add(self, elem): # 为树添加节点
node = Node(elem)
if not self.root: #如果树是空的,则对根节点赋值
self.root = node
else:
queue = []
queue.append(self.root)
while Ture: #对已有的节点进行层次遍历
cur = queue.pop(0)
if not cur.lchild:
cur.lchild = node
return
elif not cur.rchild:
cur.rchild = node
return
else:
queue.append(cur.lchild)
queue.append(cur.rchild)
|
遍历:树的两种重要的遍历模式是深度优先遍历和广度优先遍历,深度优先遍历又分为先序、中序和后序,本文给出广度优先遍历方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| def breadth_travel(self): # 从树的root开始,从上到下从从左到右遍历整个树的节点
if not self.root:
return
queue = []
queue.append(self.root)
while queue:
node = queue.pop(0)
print(node.elem, end=" ")
if node.lchild:
queue.append(node.lchild)
if node.rchild:
queue.append(node.rchild)
if __name__ == '__main__':
tree = BinaryTree()
tree.add(0)
tree.add(1)
tree.add(2)
tree.add(3)
tree.add(4)
tree.add(5)
tree.add(6)
tree.add(7)
tree.add(8)
tree.add(9)
print("广度优先遍历(层次遍历):", end=" ")
tree.breadth_travel()
|
运行结果:
1
| 广度优先遍历(层次遍历): 0 1 2 3 4 5 6 7 8 9
|

